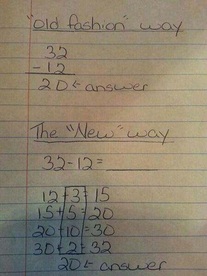
Hold up, I'm calculatin' ... because Common Core are awesome. Yes, I no that aint no proper grammar, but so long's I got the IDEA right, it'r be cool. I still'll get hired someplace that don't care bout it taken me 10 minutes to count back change in a good-speakin' way, y'all.
Lately, there's been a Common Core hate link circulating social media - it outlines the "Old Fashion" and "New Way" of calculating basic arithmetic, showing a simple math equation of 32-12. Most people over the age of 10 can simply look at the written equation and automatically reply that the answer is 20, just by doing the math in their heads - which is inarguably the fastest, most intelligent method to utilize.
But Common Core math wants people to think outside their brains. Using a linear scale, a student is supposed to work upwards through the numbers to "calculate" the correct answer. It requires the dissection of the primary equation into several other equations, which means the introduction of new numbers to those equations, and ultimately, the addition of those numbers for a math question that started as subtraction problem. Sound complicated? It is. Better have a pencil and paper handy to work it out.
Common Core advocates say that, by using this method, a student is showing an understanding of how the numbers work. They argue that this is especially beneficial to students that don't understand the concept of number placement (tens, hundreds, thousands). Additionally, by understanding how numbers work in sequence, students can more easily transition into higher forms of math, like algebra.
It's a noble concept - but it's flawed.
Because, in basic math, numbers are finite. The answers are finite. This is why we can memorize multiplication tables - the answers will not change. Ever. 1+1=2. Always. And when answers are finite, the simplest, most direct method to obtaining those answers is (or should be) the correct method. What I'm getting at is this: if the method of doing math in your head was in an epic evolutionary Natural Selection battle with Common Core, the former would win. Because math in your head is easier. Faster. Fit for everyday use.
Common Core math, by this rationale, is utterly archaic, despite its being hailed as an educational break through. Dissecting a math equation to down to a cave-man counting method isn't going to enhance the mathematical prowess of a student. In fact, I would argue that using a number line to count out a math problem is a crutch. Instead of encouraging a student to remember basic math sums, and how numbers can work in columns, we're asking them to go outside their intuitive thought process -- and rationalize it. In order for a student to apply Common Core problem solving, they would need to complicate something that could be very simple. They need paper and pencil to show and track the equations. We're asking students to stop the automatic answer - to stop their thought process - and programing them to double think something that is an earthen, finite concept...
And what would be the rationale behind getting the new generations of American citizens to double-think something as finite as whole numbers and basic math? Well - if you can double think 1+1=2, maybe you can double think free economy. Capitalism. Perhaps even morals. Even the basic constructs of freedom. I realize that's a leap in today's world... but over generations, is it really so far fetched?
But Common Core math wants people to think outside their brains. Using a linear scale, a student is supposed to work upwards through the numbers to "calculate" the correct answer. It requires the dissection of the primary equation into several other equations, which means the introduction of new numbers to those equations, and ultimately, the addition of those numbers for a math question that started as subtraction problem. Sound complicated? It is. Better have a pencil and paper handy to work it out.
Common Core advocates say that, by using this method, a student is showing an understanding of how the numbers work. They argue that this is especially beneficial to students that don't understand the concept of number placement (tens, hundreds, thousands). Additionally, by understanding how numbers work in sequence, students can more easily transition into higher forms of math, like algebra.
It's a noble concept - but it's flawed.
Because, in basic math, numbers are finite. The answers are finite. This is why we can memorize multiplication tables - the answers will not change. Ever. 1+1=2. Always. And when answers are finite, the simplest, most direct method to obtaining those answers is (or should be) the correct method. What I'm getting at is this: if the method of doing math in your head was in an epic evolutionary Natural Selection battle with Common Core, the former would win. Because math in your head is easier. Faster. Fit for everyday use.
Common Core math, by this rationale, is utterly archaic, despite its being hailed as an educational break through. Dissecting a math equation to down to a cave-man counting method isn't going to enhance the mathematical prowess of a student. In fact, I would argue that using a number line to count out a math problem is a crutch. Instead of encouraging a student to remember basic math sums, and how numbers can work in columns, we're asking them to go outside their intuitive thought process -- and rationalize it. In order for a student to apply Common Core problem solving, they would need to complicate something that could be very simple. They need paper and pencil to show and track the equations. We're asking students to stop the automatic answer - to stop their thought process - and programing them to double think something that is an earthen, finite concept...
And what would be the rationale behind getting the new generations of American citizens to double-think something as finite as whole numbers and basic math? Well - if you can double think 1+1=2, maybe you can double think free economy. Capitalism. Perhaps even morals. Even the basic constructs of freedom. I realize that's a leap in today's world... but over generations, is it really so far fetched?
 RSS Feed
RSS Feed
